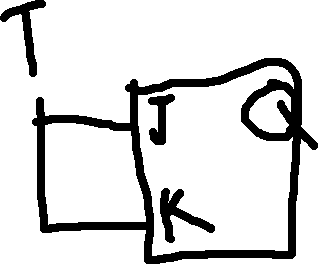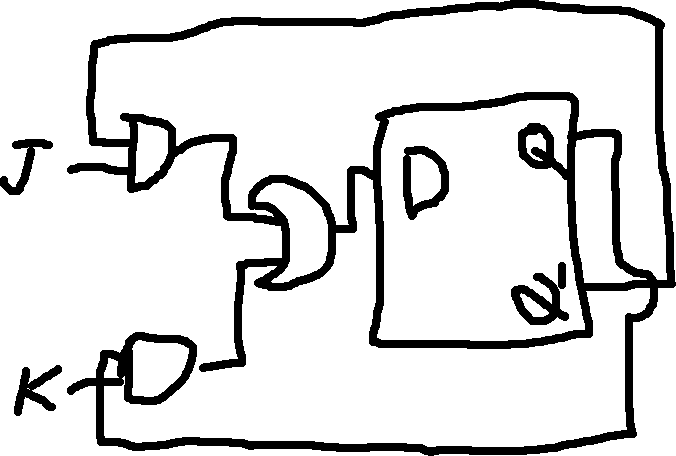
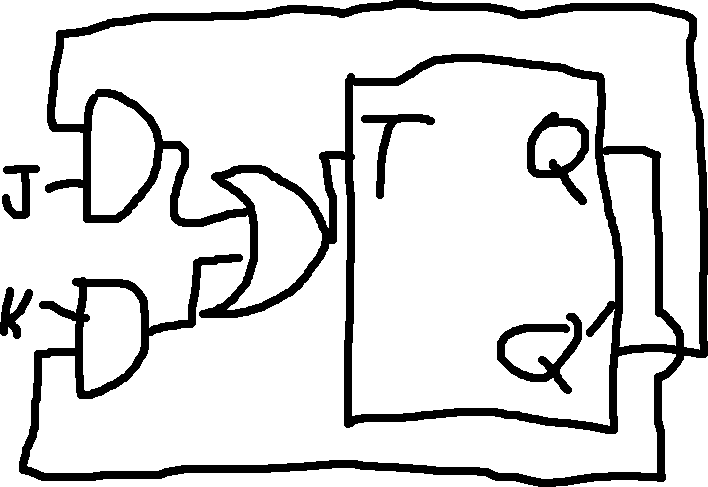
You can convert one type of flip-flop to another by modifying its input logic.
This often involves creating a conversion table and using logic simplification techniques like K-maps to determine the required input connections.
| T | Q \to Q^+ | D |
|---|---|---|
| 0 | 0 \to 0 | 0 |
| 0 | 0 \to 1 | 1 |
| 1 | 1 \to 0 | 1 |
| 1 | 1 \to 1 | 0 |
Observation:
| D | Q \to Q^+ | T |
|---|---|---|
| 0 | 0 \to 0 | 0 |
| 0 | 1 \to 0 | 1 |
| 1 | 0 \to 1 | 1 |
| 1 | 1 \to 1 | 0 |
Observation:
| J | K | Q \to Q^+ | D |
|---|---|---|---|
| 0 | 0 | 0 \to 0 | 0 |
| 0 | 0 | 1 \to 1 | 1 |
| 0 | 1 | 0 \to 0 | 0 |
| 0 | 1 | 1 \to 0 | 0 |
| 1 | 0 | 0 \to 1 | 1 |
| 1 | 0 | 1 \to 1 | 1 |
| 1 | 1 | 0 \to 1 | 1 |
| 1 | 1 | 1 \to 0 | 0 |
Observed Minterms:
Now, let’s create a k-map to find a simple answer.
| j’k’ | j’k | jk | jk’ | |
|---|---|---|---|---|
| q’ | 1 | 1 | ||
| q | 1 | 1 |

| J | K | Q \to Q^+ | T |
|---|---|---|---|
| 0 | 0 | 0 \to 0 | 0 |
| 0 | 0 | 1 \to 1 | 0 |
| 0 | 1 | 0 \to 0 | 0 |
| 0 | 1 | 1 \to 0 | 1 |
| 1 | 0 | 0 \to 1 | 1 |
| 1 | 0 | 1 \to 1 | 0 |
| 1 | 1 | 0 \to 1 | 1 |
| 1 | 1 | 1 \to 0 | 1 |
Minterms:
| j’k’ | j’k | jk | jk’ | |
|---|---|---|---|---|
| q’ | 1 | 1 | ||
| q | 1 | 1 |
The maxterms from this k-map are:
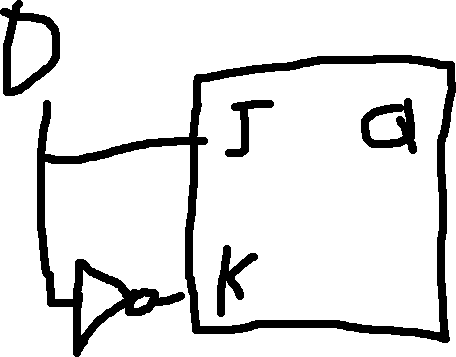
| D | Q \to Q^+ | J | K |
|---|---|---|---|
| 0 | 0 \to 0 | 0 | X |
| 0 | 1 \to 0 | X | 1 |
| 1 | 0 \to 1 | 1 | X |
| 1 | 1 \to 1 | X | 0 |
Why? Recall this k-map:
Q \to Q^+ J K 0 \to 0 0 0 0 1 0 X 0 \to 1 1 0 1 1 1 X 1 \to 0 0 1 1 1 X 1 1 \to 1 0 0 1 0 X 0
Observations:
| T | Q \to Q^+ | J | K |
|---|---|---|---|
| 0 | 0 \to 0 | 0 | X |
| 0 | 1 \to 1 | X | 0 |
| 1 | 0 \to 1 | 1 | X |
| 1 | 1 \to 0 | X | 1 |