Majority Function: A 2/3 of the bits must be 1 to output 1.
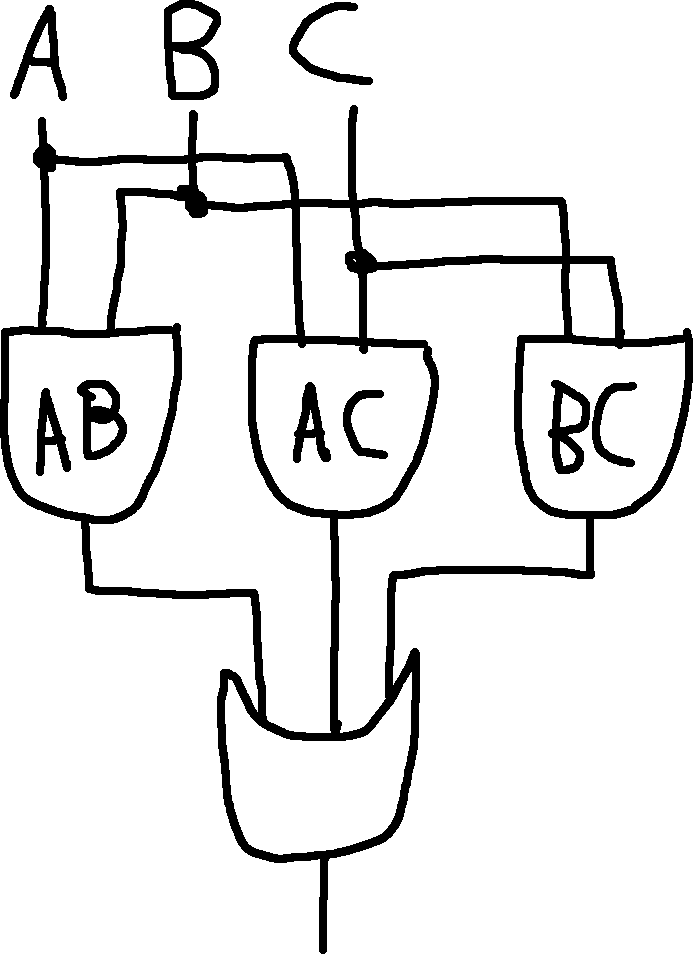
- AB + AC + BC
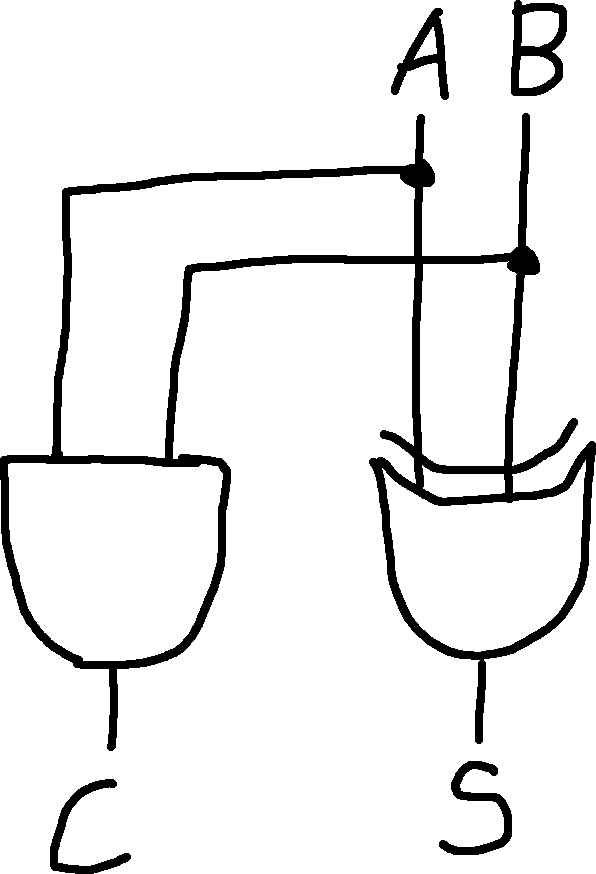
Half Adder: Digital logic circuit that performs binary addition of two single-bit binary numbers.
Behavior:
\begin{align*} \begin{align*} & 0 \\ + & 0 \\ = & 00 \end{align*} \qquad & \qquad \begin{align*} & 0 \\ + & 1 \\ = & 01 \end{align*} \\ \begin{align*} & 1 \\ + & 0 \\ = & 01 \end{align*} \qquad & \qquad \begin{align*} & 1 \\ + & 1 \\ = & 01 \end{align*} \end{align*}
Rewritten as a truth table:
| A | B | Carry | Sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Observations:
Note: Remember to think of the logic gates as minimum and maximum functions!
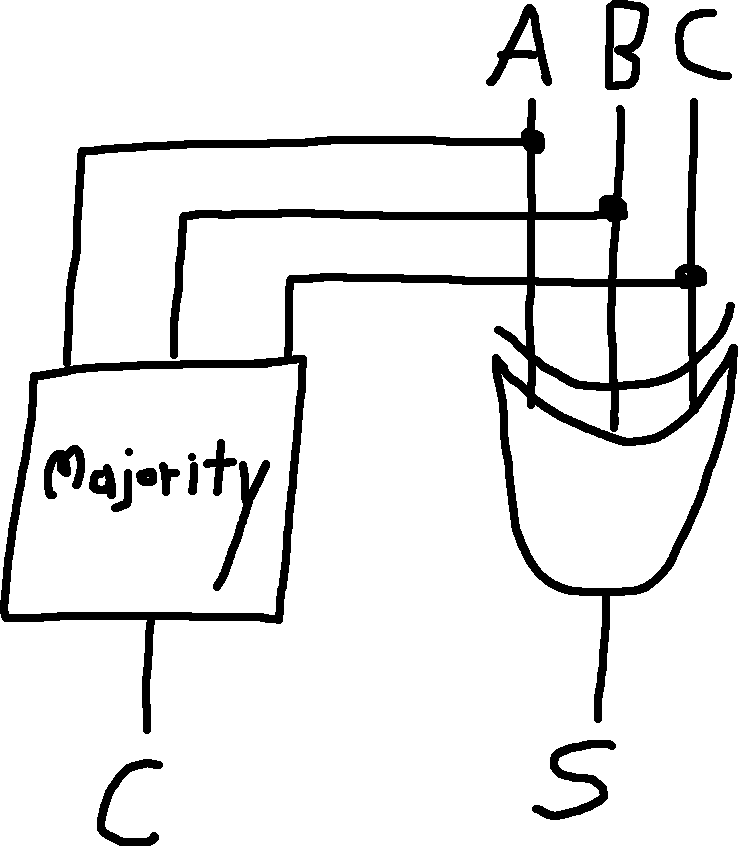
Full Adder: Like a half adder, except it adds 3 bits instead of 2 bits.
Behavior:
\begin{align*} \begin{align*} & 0 \\ + & 0 \\ + & 0 \\ = & 00 \end{align*} \qquad & \qquad \begin{align*} & 0 \\ + & 0 \\ + & 1 \\ = & 01 \end{align*} \qquad & \qquad \begin{align*} & 0 \\ + & 1 \\ + & 0 \\ = & 01 \end{align*} \\ \begin{align*} & 0 \\ + & 1 \\ + & 1 \\ = & 10 \end{align*} \qquad & \qquad \begin{align*} & 1 \\ + & 0 \\ + & 0 \\ = & 01 \end{align*} \qquad & \qquad \begin{align*} & 1 \\ + & 0 \\ + & 1 \\ = & 10 \end{align*} \\ & & \begin{align*} & 1 \\ + & 1 \\ + & 1 \\ = & 11 \end{align*} \end{align*}
Truth Table:
| A | B | C | Carry | Sum |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Observations:
Majority Function: A 2/3 of the bits must be 1 to output 1.
- AB + AC + BC
In a positional system, the value of a digit is the digit \times place value. The total value is the sum of these products.
To denote positional value in binary, we can chain the carry-bit into another addition procedure.
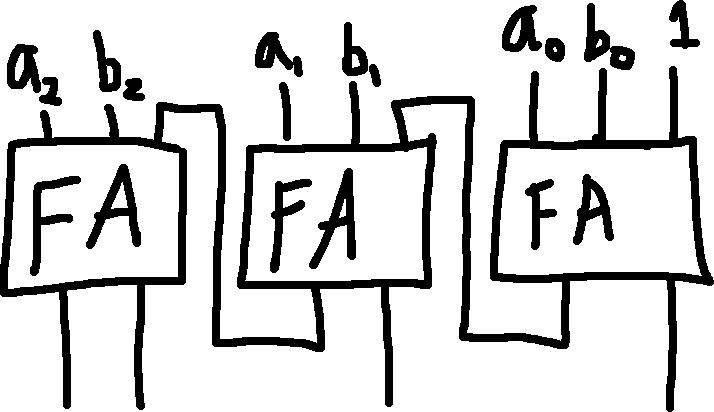
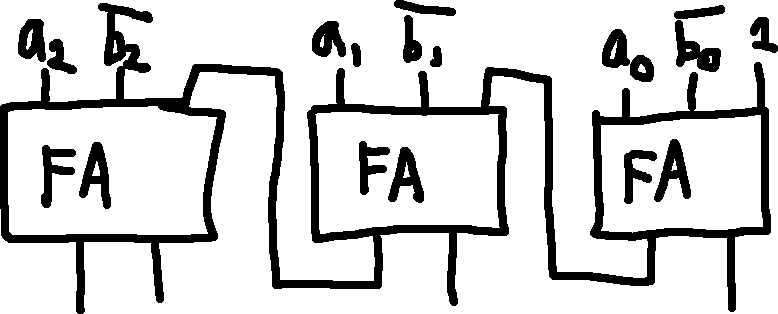
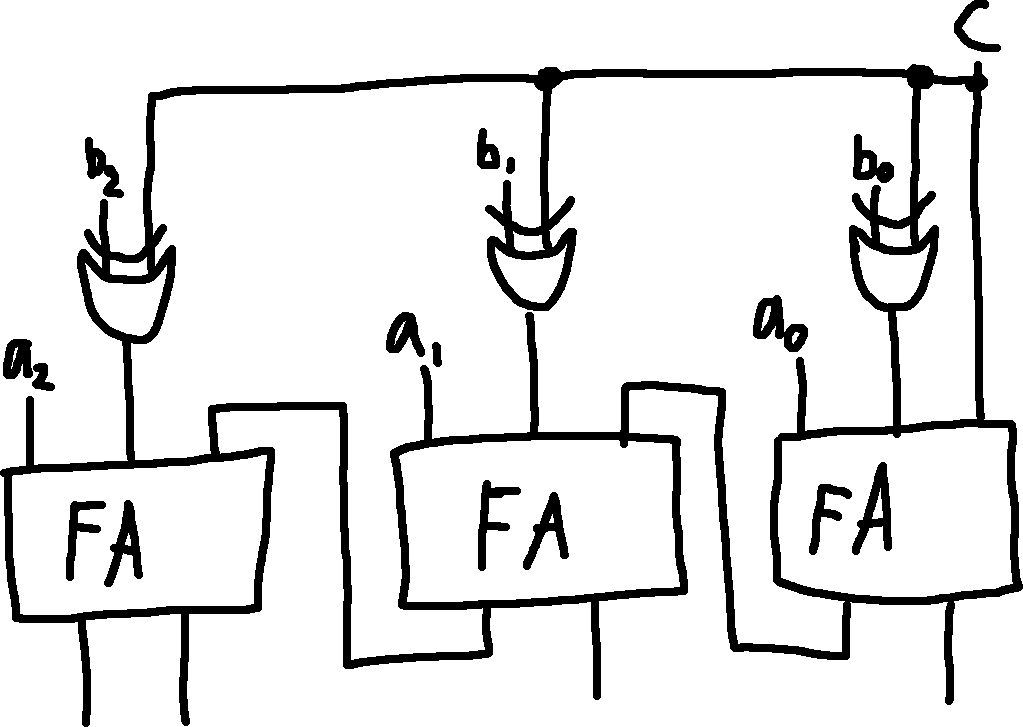
Step-by-step addition of two 3-bit numbers:
Variation with HA: You could also do step 1 with a HA to save electricity and improve speed, but using a FA makes the design cascadeable.
- e.g., you can create a 6-bit adder by connecting two 3-bit adders; or a 9-bit adder using three 3-bit adders, etc.
Recall: To get the two’s complement (negative) of a binary number, you need to apply
NOTto every bit and do+1
NOT b and put 1 into the first FA to do a + (-b)
This is an incrementer:
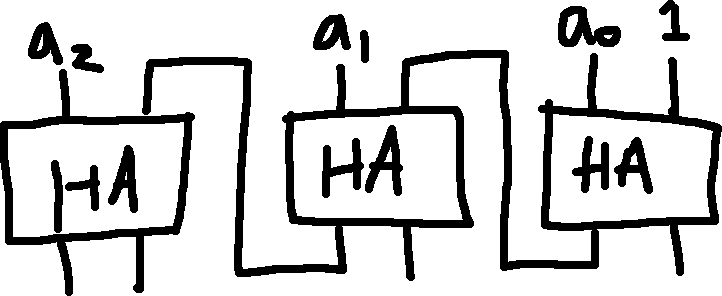
Q: What if we want to do (a-1)?
A: We just find a + (-1) (add the two’s complement of 1 to a.
Let’s find the two’s complement of a 3-bit representation of 1 to find pattern.
001_2 = 1_{10}
NOT(001_2)' = 110_2
+1\begin{align*} &110 \\ +&001 \\ =&111 \end{align*}
Thus, 111_2 = -1_{10}
Note: Alternatively, we could’ve used the shortcut of flipping all bits left of the rightmost
1bit (CS2640 - Two’s Complement).
Thus, a decrementer looks like this:
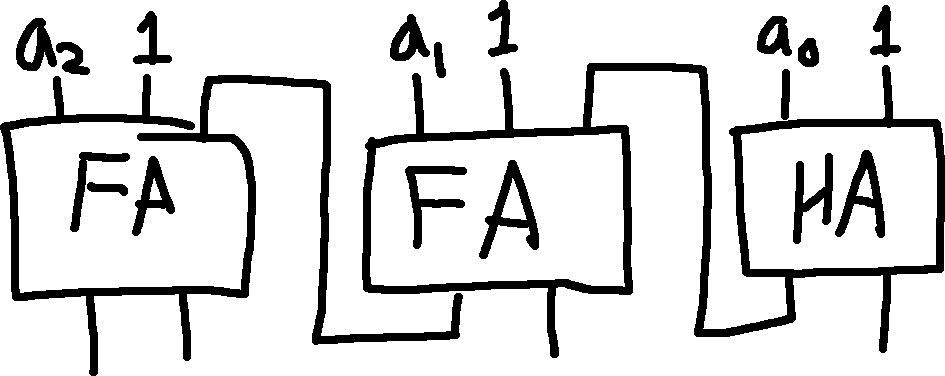
To combine the adder and subtractor, we’ll need to use this property of XOR:
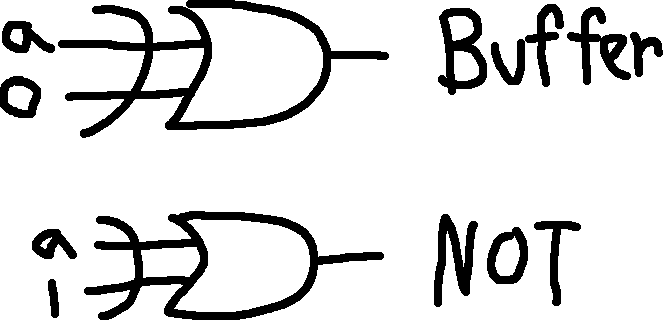
Using this switch technique, we can toggle between adding A+B and adding A+(-B).
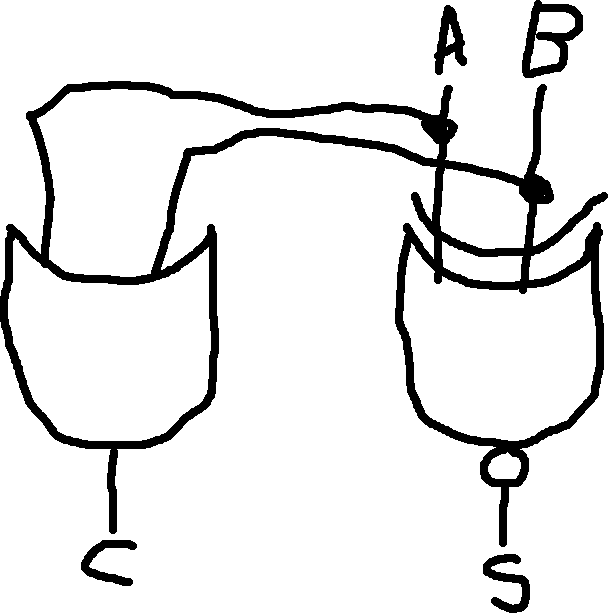
Half Adder Plus: Like a half adder, except it does A+B+1 rather than A+B.
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
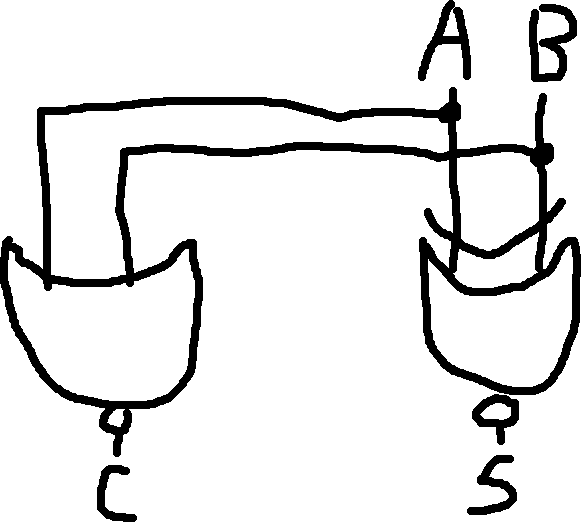
Half Adder Minus: Like a half adder, except it does A+B-1 rather than A+B.
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
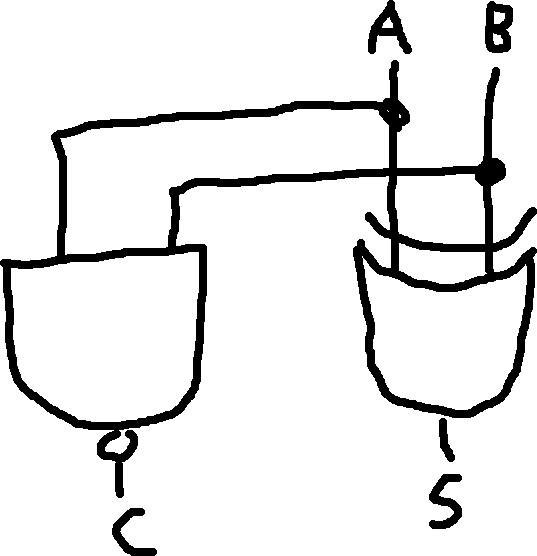
Half Adder Minus Minus: Like a half adder, except it does A+B-2 rather than A+B.
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
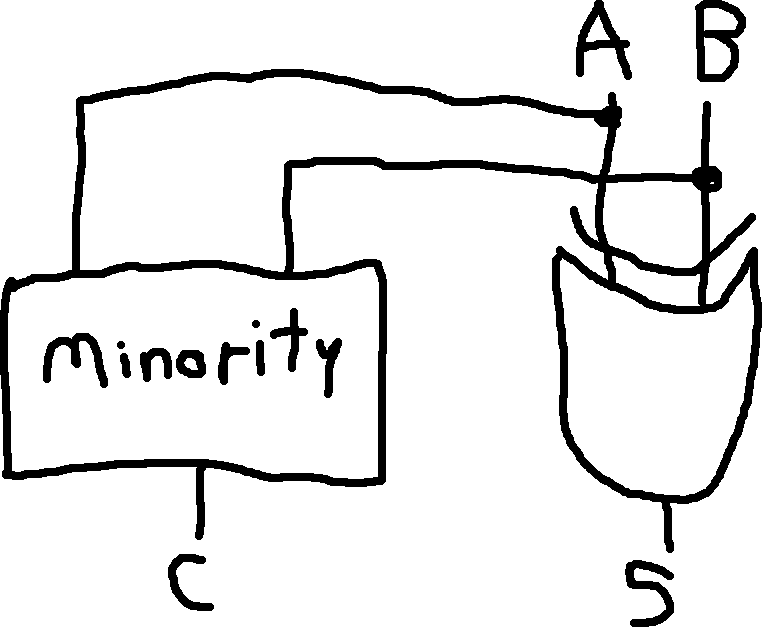
Fall Adder Minus Minus: Like a full adder, except it does A+B+C-2 rather than A+B+C.
Note: A minority gate is just the NOT of a majority gate.
| A | B | C | Carry | Sum |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Note: You can’t make FA+ or FA++ because there aren’t enough bits to represent 4_{ 10 }
Note: You can’t make FA- we can’t represent -1_{10} and 2_{10} without mixing the signed and unsigned numbers (the meaning of the MSBit becomes vague).