Buffer

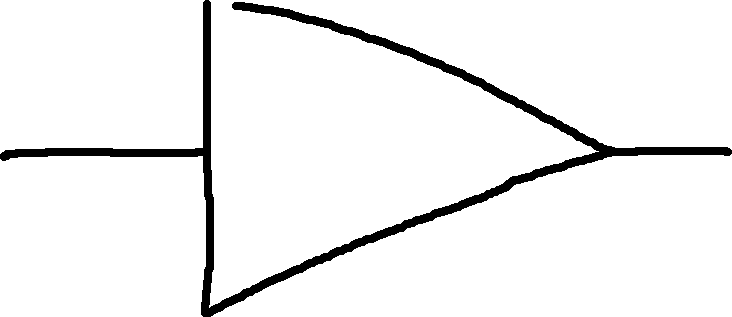
Buffer: Anything you put in, you get out.

• Normally used to amplify something.

NOT (Inverter)

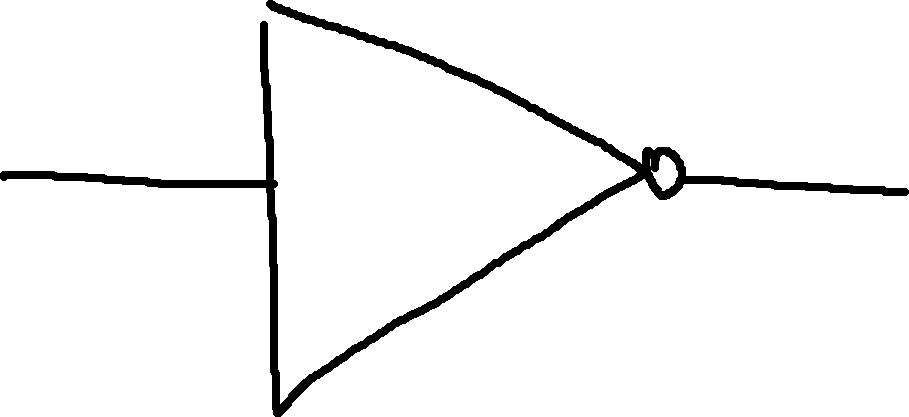
NOT: Flip the signal.

AND & OR

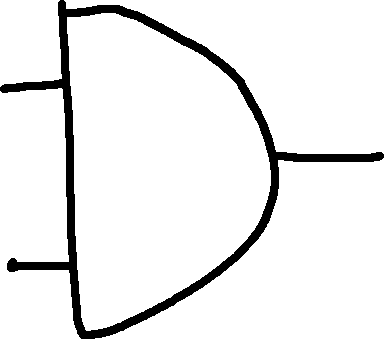
AND: If both are 1, return 1; otherwise return 0.

• Returns the minimum of inputs.

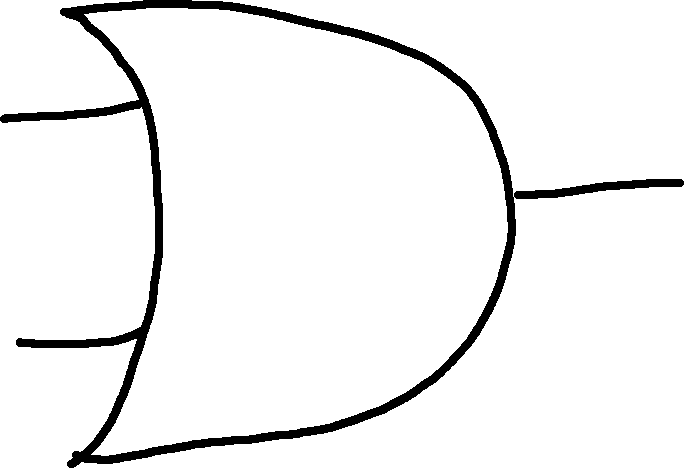
OR: Inclusive OR

• Returns the maximum of inputs.

NAND & NOR

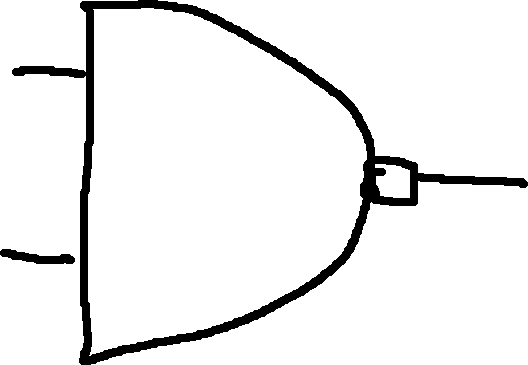
NAND: NOT AND

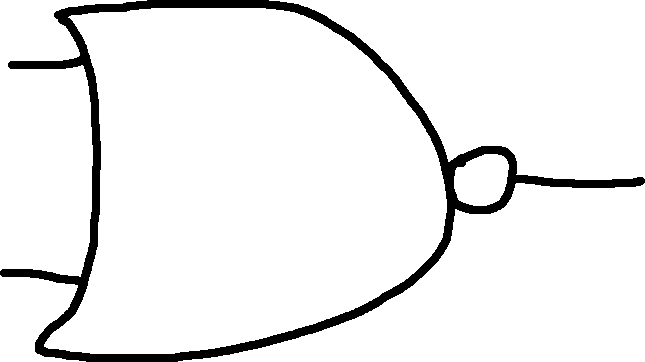
NOR: NOT OR

XOR & XNOR

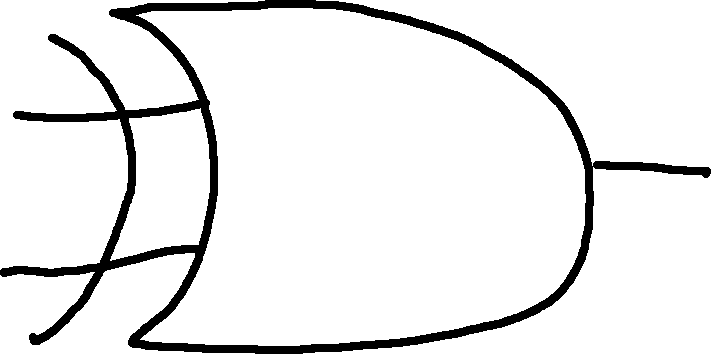
XOR: Exclusive OR

• If number of 1’s is odd, return 1.

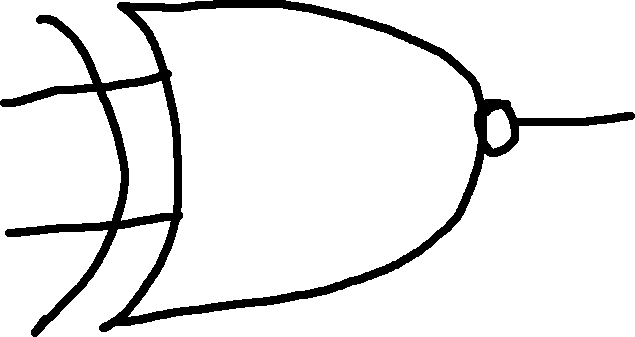
XNOR: Exclusive NOR

• If number of 1’s is odd, return 0.

Universal/Complete Gates

NAND and NOR can create all the basic logic gates.

NAND

NOT:

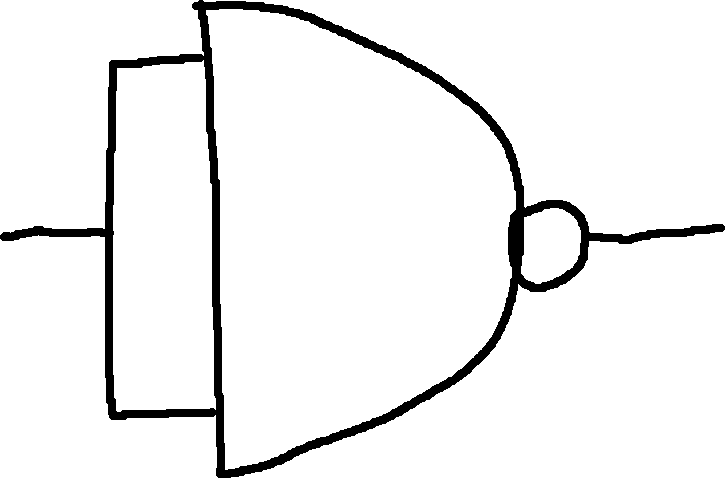
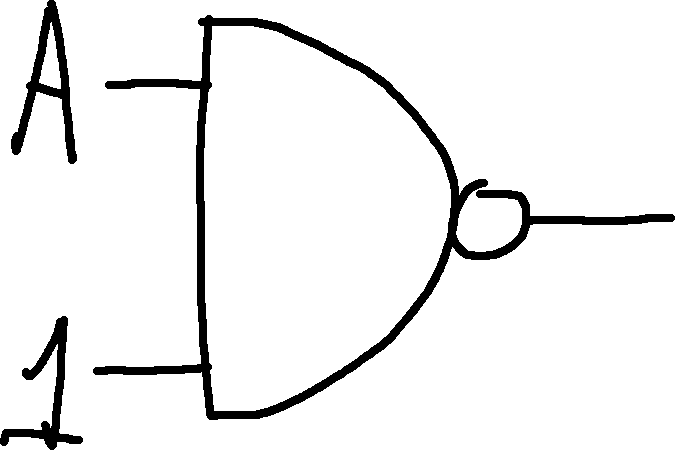
OR:

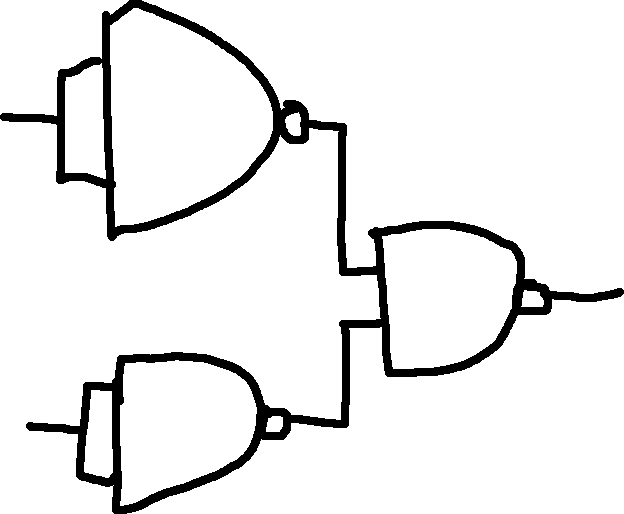
AND:

NOR

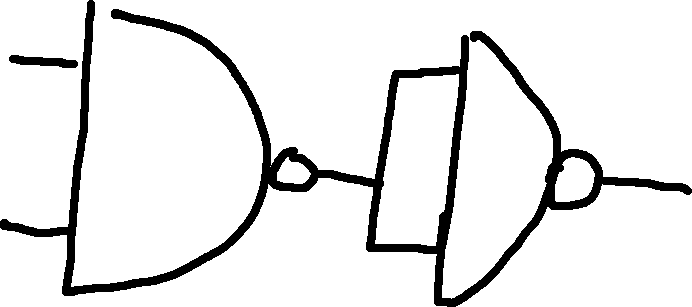
NOT:

AND:

OR:

NAND:

Multiplexer (MUX)

MUX: Functions like a switchboard.

2:1

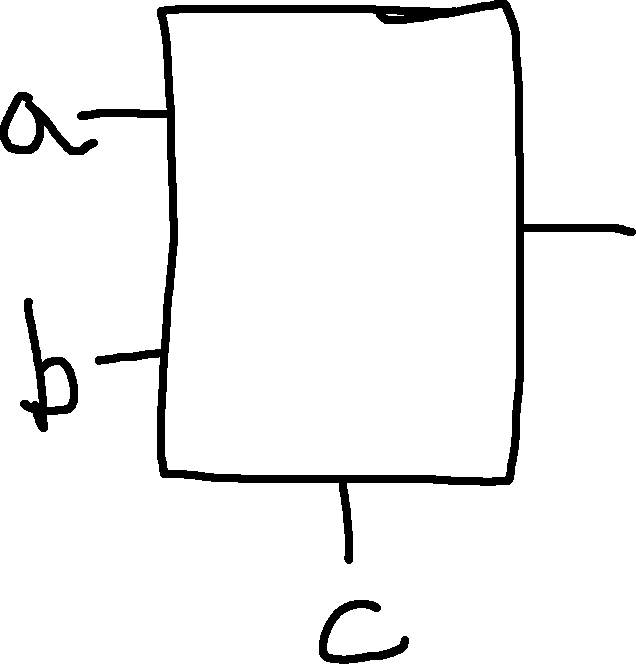
This MUX takes three inputs, a, b, and c. 

• If c is 0, a will be outputted.
• If c is 1, b will be outputted.

c'a+cb

We can make any basic logic gate with a MUX.

Example: Creating Logic Gate with a 2:1 MUX

Suppose we want to configure a MUX to give this truth table:

We want to split the table into two states first.

• For this example, a=0 and a=1 is a good split.

Observation: We can immediately see that when a=0, out is always 1, so we can draw a partial MUX like this:

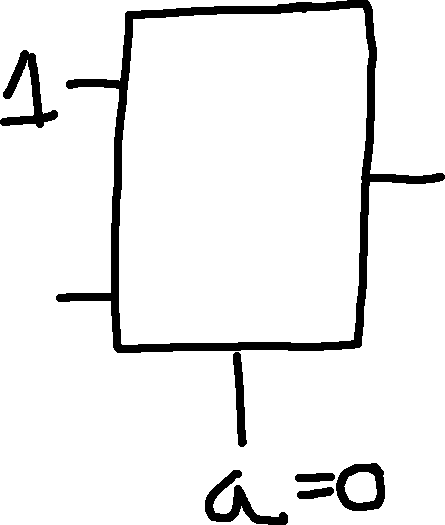
Observation: Looking at the other truth table, we can see that out is always b when a=1, so we can draw a partial MUX like this:

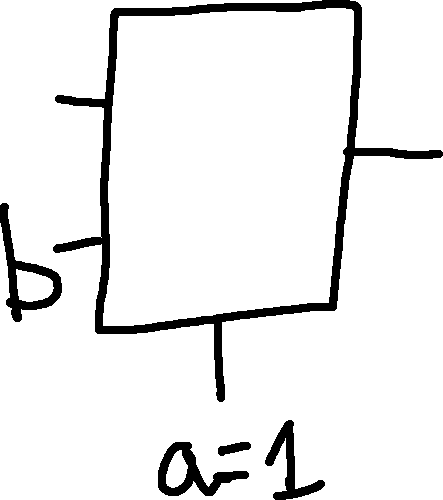
Putting it all together, the final MUX is this:

4:1

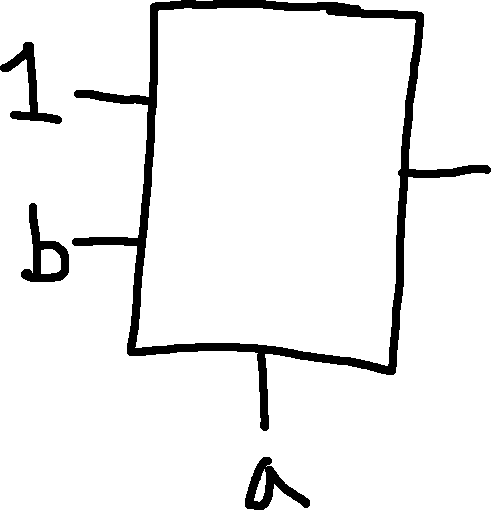
TODO draw a 4:1 MUX

This MUX takes six inputs, a, b, c, d, x, and y

When and How to Use

8:1

TODO draw a 8:1 MUX