Example: An adjacency list
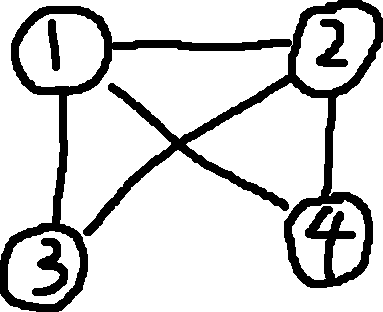
Adjacency List: 1 \to 2 \to 3 \\ 2 \to 1 \to 3 \to 4 \\ 3 \to 1 \to 2 \\ 4 \to 1 \\
NTS: Remember 2 connects to 4, 3 doesn’t connect to 4.
There are two parameters to represent, vertices and edges.
\text{Graph: } G = (V, E)
There are two methods of representation (mathematically):
List all vertices.
Properties:
- Total Size: \Theta ( |V| + |E| )
- Better on sparse graphs

Adjacency List: 1 \to 2 \to 3 \\ 2 \to 1 \to 3 \to 4 \\ 3 \to 1 \to 2 \\ 4 \to 1 \\
NTS: Remember 2 connects to 4, 3 doesn’t connect to 4.
Store vertices in a square matrix
Properties:
- Total Size: ( n^2 )
- Better on dense graphs.

| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 |
| 3 | 1 | 1 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 |
Graph Traversal: Problem of visiting all nodes in a graph in a particular manner, updating/checking values along the way.
There are two elementary traversal strategies using brute-force algorithms:
Both provide efficient ways to visit each vertex and edge, they only differ in order of visiting.
Visit vertices by always moving away from the last-visited vertex to an unvisited one. Backtracks if no adjacent unvisited vertex is available.
Data Structure: Stack (FILO)
- Vertex pushed on when it’s reached for the first time.
- Vertex popped off when it becomes a dead end (i.e., no adjacent unvisited vertex).
Example
TODO Draw graph aecfdb
Mathematically, we could phrase this as:
a_{1, 6} c_{2, 5} d_{3, 1} f_{4, 4} b_{5, 3} e_{6, 2}
Note: First subscript is the order something was popped-on, second subscript is order it was popped-off.
We aren’t done though, there’s the other portion to traverse:
g_{1,4} h_{2,3} i_{3,2} j_{4,1}
Now, we are truly done.
TODO
You can use the traversal’s stack to construct a tree-like graph, which we’ll call a DFS forest.
DFS Forest:
Example: Graph to Stack to Forest
TODO Diagram
The traversal stack is: TODO
Constructing the DFS Forest from this stack, we get: TODO
For us, we’ll just look at the original graph to determine back-edges, as determining this from the traversal stack is a little more involved.
- We just use the traversal stack to build the easier tree edges.
Visit verticies by moving across to all neighbors of last-visited vertex.
TODO Explain
Data Structure: Uses queue
Similar to a level-by-level tree traversal
More Notes:
You can use the traversal’s queue to construct a tree-like graph.
TODO Example