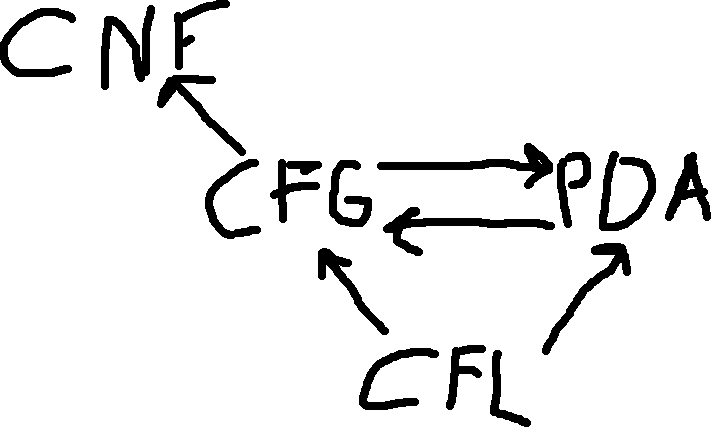
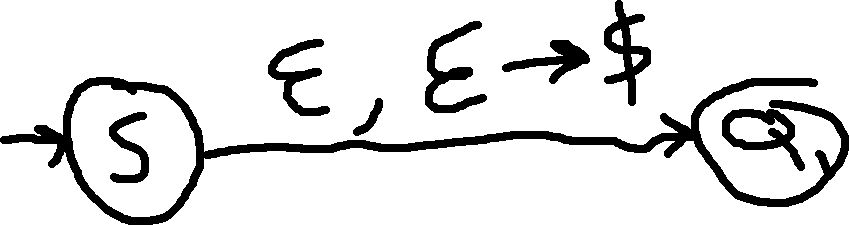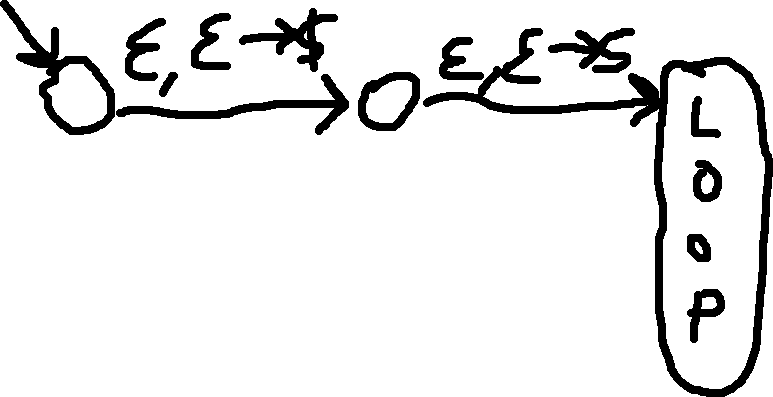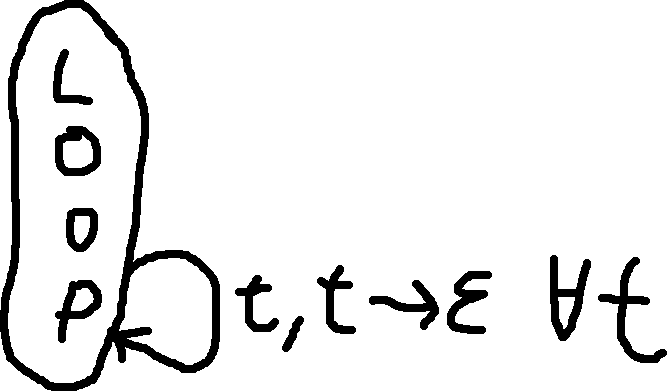Pushdown Automata
On Pushdown Automaton v. Finite Automaton:
A finite automaton reads a single tape of input in one direction.
A pushdown automaton also reads an input tape, but it also has an additional tape that it can read and write to.
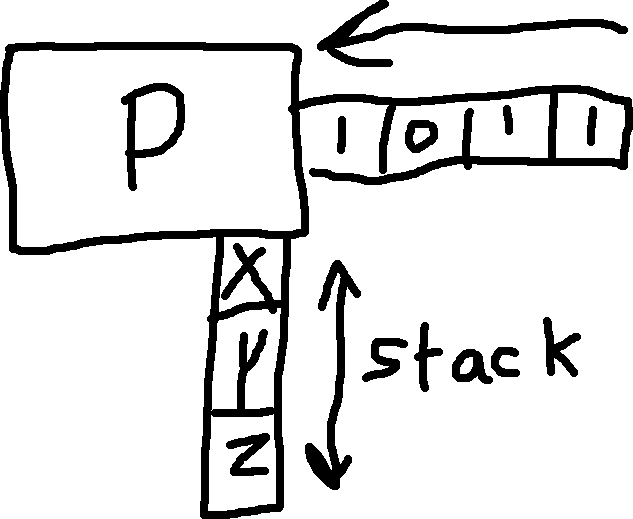
Stack: A PDA can write and read symbols to the stack.
- Writing a symbol “pushes down” all other symbols on the stack.
- Reading a symbol removes it from the top, moving all the symbols back up.
Push In Notation (r,o \to i)
Example: r,o \to i

- This transition means we can go from state 1 to 2 by:
- Reading r,
- Popping out “o” from the stack, and
- Pushing in “i” to the stack.
Formal: Let \Gamma be an alphabet, then:
- o, i \in \Gamma_\epsilon = \Gamma \cup \{ \epsilon \}
- (because we can also push and pop epsilon)
Example: Marking End of Stack
- We like to push $ to the stack at the start to indicate the end.
Examples
Example: Simple PDA
- Q: Write a PDA that reads a string of { a^n b^n }
- A: Our solution will be to push “0” every time we read “a” and pop “0” every time we read “b”, and using a sentinel value to verify |a| = |b| = n
eps
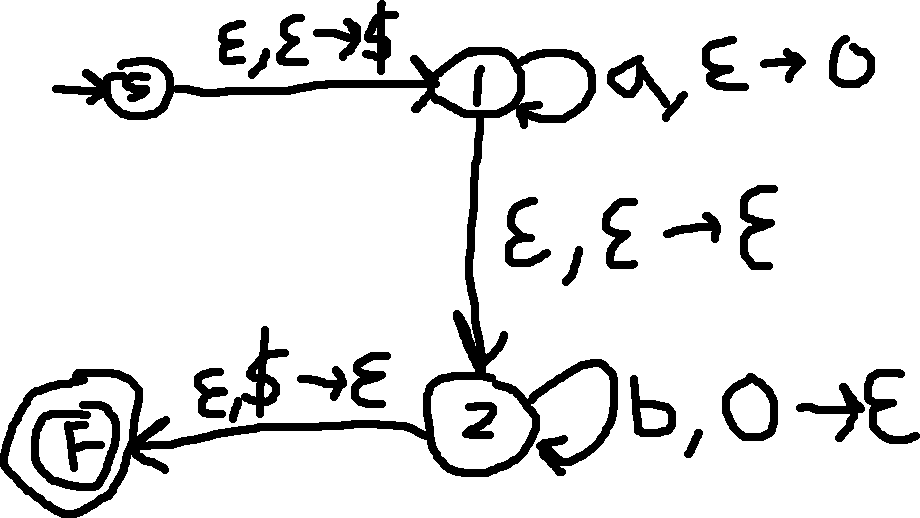
- We use transitions to limit the strings we can accept.
- Notice how we never counted the variables, we just used the simplest hardware
Example: Write a PDA that accepts { a^n b^{3n} }
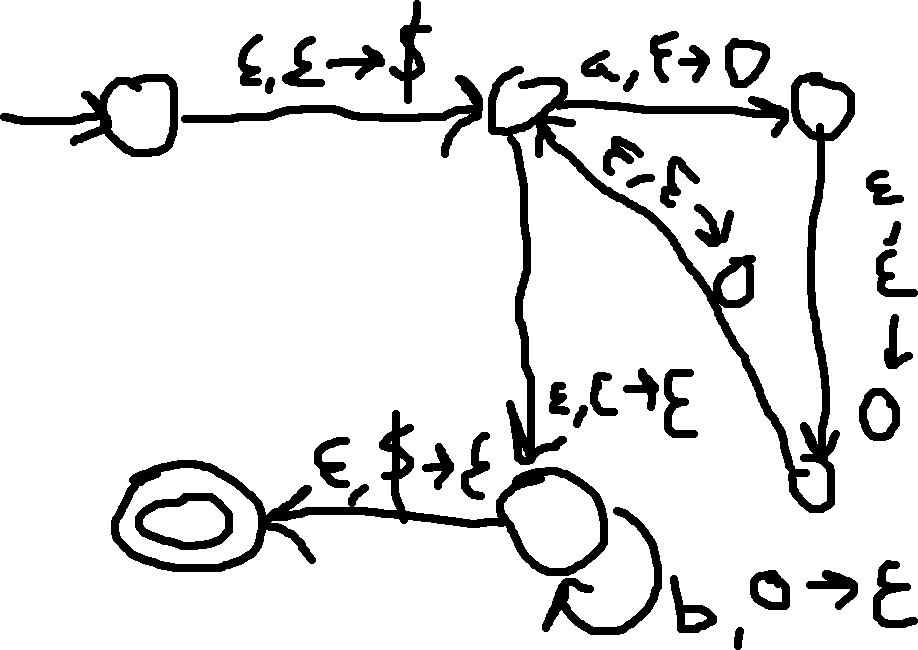
Example: Write a PDA that accepts { a^n b^{3n+1} }
- In the above photo, we can replace the \epsilon, \epsilon \to \epsilon between the a and b loop with b, \epsilon \to \epsilon to require +1 b.
Example: Write a PDA that accepts { a^n b^{m} | m \ge 3 }
- Q: We can rewrite this as { a^n b^{3n} b^k | k \ge 0 }
- A: Use the PDA from { a^n b^{3n} }, but put a self-loop on the accepting state that is b, \epsilon \to \epsilon
What We Need to Know
A pushdown automaton is a 6-tuple (Q, \Sigma, \Gamma, \delta, q_0, F) where:
- Q: Set of states
- \Sigma: Input alphabet
- \Gamma: Stack alphabet.
- \delta: Q \times \Sigma_\epsilon \times \Gamma_\epsilon \to P(Q \times \Gamma_\epsilon) is transition function
- q_0 \in Q: Start state
- F \subseteq Q
Q, \Sigma, \Gamma, and F are finite.
Generic Grammar to PDA
Example
Suppose the grammar
S \to a^2 S b | \epsilon
We’ll write the parse tree:
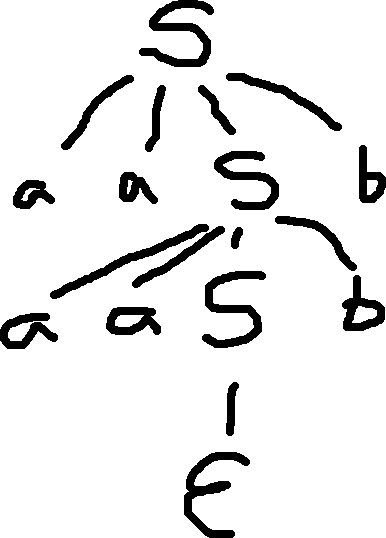
We will begin copying the parse tree onto a PDA’s stack tape now:
From layer one we have:
When we read a terminal, we want to pop it off the stack. e.g.,
- a, a \to \epsilon
- b, v \to \epsilon
to
When we read a variable, we have to expand it.
- In this case, after reading two a’s, S can either be expanded into
aaSb or \epsilon
Suppose we’ve read two as and now have to expand S.
- Pop S (\epsilon, \epsilon \to S)
- Push b (\epsilon, b \to \epsilon)
- Push S (\epsilon, S \to \epsilon)
- Push a (\epsilon, a \to \epsilon)
- Push a (\epsilon, a \to \epsilon)
The PDA so far looks like:
- Push $
- Push S
- Major Loop:
- Pop S
- Push b
- Push S
- Push a
- Push a
- Read a, pop a (x2)
- Major Loop OR just pop S and push epsilon.
Finally, to account for b, we just read the right number of bs and then pop $ to reach the accepting state.
Steps
- Push $ and start variable
- This goes to a large loop state.
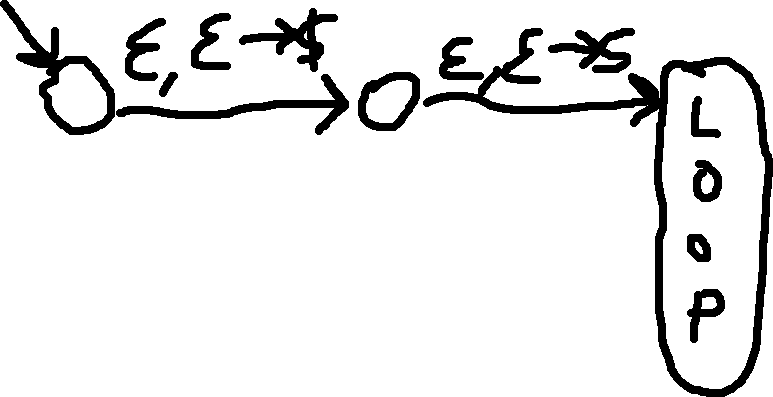
- \forall rule: A \to w:
- pop A, and push w^R (push W in reverse)
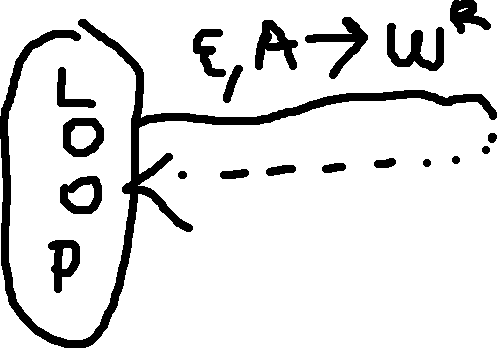
- \forall t \in \Gamma:
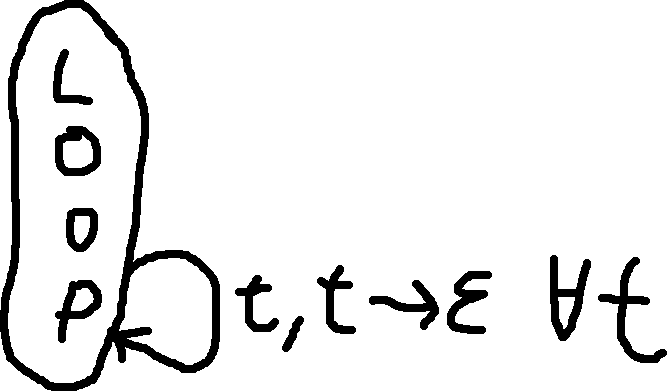
- \epsilon, \$ \to \epsilon from loop to accept.
More Examples
A
S \to aTb|b \\
T \to Ta|\epsilon
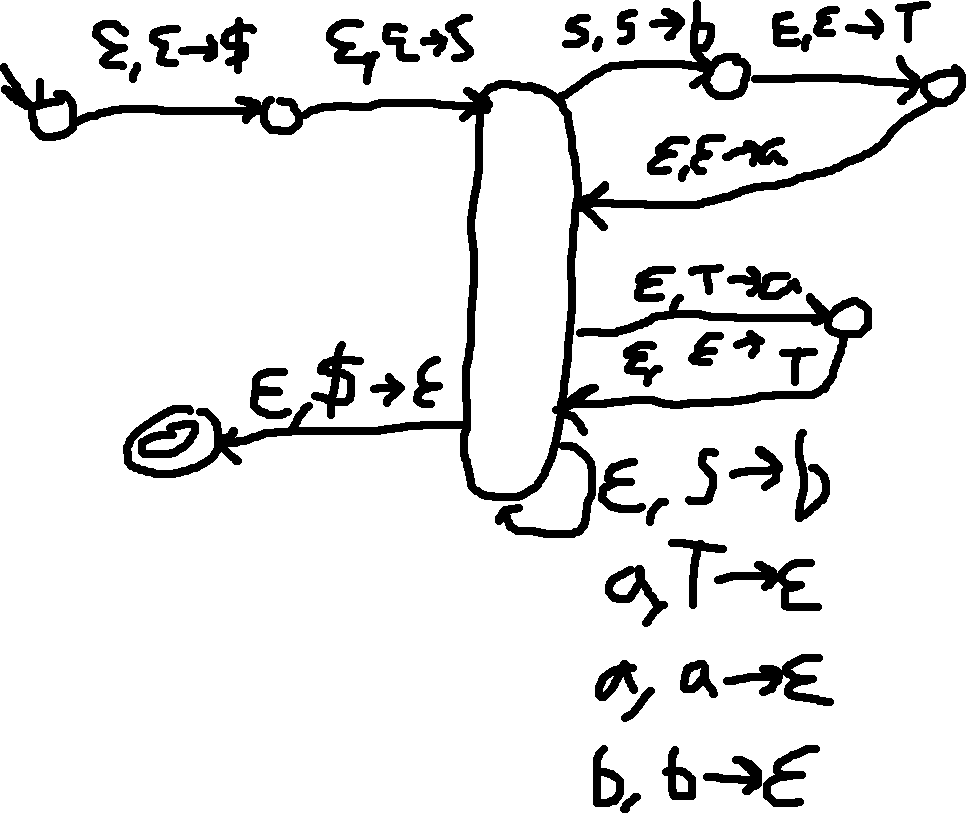
- Correction: \epsilon, T\ to a should be T, T\ to a
B
a^i b^j c^k | i,j,k \ge 0 \text{ and } i = h \lor i = k
Divide and conquer.