Context-Free Grammars

Context-Free Grammar

Layman Explanation

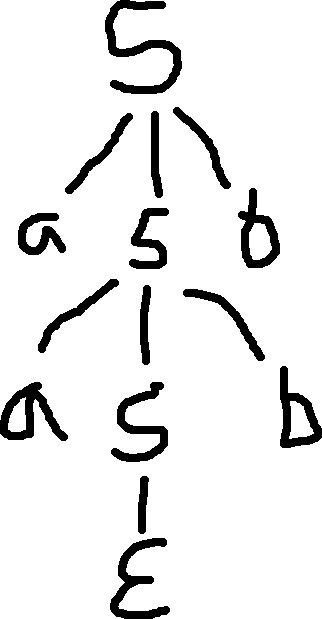
Suppose the following CFG:

S \to a S b \\~\\ S \to \epsilon

S can render/derive/transform into aSb or \epsilon

This is the parse tree of S:

Why: S \to a S b \to aa S bb \to aaa S bbb \to aaa \epsilon bbb

In other words, this grammar can render anything in { a^n b^n }, which is the language the grammar generates.

Notation: L(G) : Language of the grammar

Formal Definition

Formal Definition of CFG: G: (V, \Sigma, R, S)
V: Finite set of variables
\Sigma: Finite set of terminals. Disjoint from V.
R: Set of rules
S: The start variable (S \in V)

If u, v, and w are strings of variables and terminals, and A \to w is a rule of the grammar, we say that uAv yields uwv, written uAV \Rightarrow uwv

Say that u derives v, written u \Rightarrow v, if u = v or if a sequence u_1,u_2,...u_k exists for k \ge 0 and

u \Rightarrow u_1 \Rightarrow u_2 \Rightarrow ... \Rightarrow u_k \Rightarrow v

Language of the Grammar: { w \in \Sigma^* | S \overset{*}{\Rightarrow} w }

Q: What does the following CFG render?
S \to a S \\ S \to S b \\ S \to \epsilon
A:
This example doesn’t enforce the # of as to be equal to bs (not {a^n b^n})
Renders: \epsilon, a, b, ab, aa, bb, ...
Thus: L(G) = { a^* b^* }

Q: Define a CFG for {a^{3n}}
A:
We want to generate the terminal in threes at a time, so:
S \to S aaa \\ S \to \epsilon
shorter: S \to S a^3 | \epsilon

Designing CFGs

Linked Strings

If your language has two substrings that are “linked”:

R \to uRv

Linked Substrings?: When the machine needs to remember an unbounded amount of information to count the substrings to satisfy some relationship.
e.g., { a^n b^n }

Ambiguity

Ambiguity: A string w is derived ambiguously by a CFG (G) if it has \ge 2 leftmost derivations.
G is ambiguous if it generates some string ambiguously.

Sometimes a grammar can generate the same string in many ways.

This can be undesirable for applications like programming languages.
In this case, many parse trees can be made for the same grammar.

Example: (EXPR) \to (EXPR) + (EXPR) | (EXPR)\times(EXPR) | (EXPR) | a
This is ambiguous

Q: How to avoid ambiguity?
A: Separate by using different variables
e.g., this is an unambiguous grammar \begin{align*} (EXPR) &\to (EXPR) + (TERM) | (TERM) \\ (TERM) &\to (TERM) \times (FACTOR) | (FACTOR) \\ (FACTOR) &\to (EXPR) | a \end{align*}

Inherently Ambiguous: Some languages can only be generated by ambiguous grammars.
e.g., English

Conversion Examples

NFA to CFG

Look at the individual states and generate tiny grammars for them.
This is essentially the ripping-out process.
Accepting states go to epsilon.

Q: Convert the NFA to CFG
A: Q1 \to a Q2 \\ Q2 \to a Q3 \\ Q3 \to a Q1 \\ Q1 \to \epsilon

Q: Convert the NFA to CFG
A: S \to aA \\ A \to aS | bA | F \\ F \to aA | bF | \epsilon

Language to CFG

Remember: Divide and conquer! (concatenate and union)

Q: { a^n ( b^3 )^n }

A: S \to a S b^3 | \epsilon

Q: { a^n ( bcd )^n }

A: S \to a S bcd | \epsilon

Q: { a^n b^n | n <= 3 }

A: S \to \{ \epsilon | a b | a^2 b^2 | a^3 b^3 \}

Q: { a^n b^n | n >= 2 }

A: S \to \{ a^2 S b^2 | \epsilon \}

Q: { w | w has n a’s and n b’s }

A: S \{ a S b | b S a | ab S | ba S | S ab | S ba | \epsilon \}, or
A: S \{ a S b | b S a | S S | \epsilon \} (simplified)
This form is useful for mixed orders.

Q: { w | w has m a’s and n b’s and m+n = 2k for some integer k >= 0 }

Chomsky Normal Form (CNF)

A CFG is in Chomsky normal form if every rule is of the form:
\boxed{ \text{CNF: } \begin{cases} A &\to BC \\ A &\to a \end{cases} }
Each production rule can only point to:
Two variables (that aren’t start variable), or
A single terminal
Start variable is the only one that can go to epsilon (S \to \epsilon)
Though it isn’t required.
We don’t want epsilon in intermediate productions.

Converting to CNF

Steps:

Start variable on left only.
- Step: New S_0 \to S
Only S_0 can (optionally) go to \epsilon.
- Step: Remove \epsilon-rules (\forall A \to \epsilon, add new rule(s) \forall A \in \text{RHS})
Ensure variables on RHS show up in pairs (A \to BC)
- Step: Remove unit rules.
  1. \forall A \to B, replace B with its rules
  2. Remove A \to A (empty steps)
Ensure single terminal on RHS (A \to a)
- Step: Add new rules. Let A \to w:
  1. If |w| > 1 and has terminals, replace every terminal with a variable.
  2. If |w| > 2 and has only variables, do binary replacements until |w| = 2

More On Rule 4:
Convention for Replacing Terminals: Suppose A \to bc BA
By convention, we can use T to organize terminals, e.g.,
A \to T_b T_c BA \\ T_b \to b \\ T_c \to c \\
Convention for Replacing Variables: Suppose A \to T_b T_c BA
By convention, we can use V to organize variables, e.g.,
A \to V_{BC} V_{BA} \\ V_{BC} \to T_b T_c \\ V_{BA} \to B A \\

Note: If something is in CNF, don’t waste time modifying it!

Purpose of CNF:

Look at this language and its empty productions.

S \to A \\ A \to B \\ B \to \epsilon

What about this loop of empty productions.

S \to A | \epsilon \\ A \to B \\ B \to S

Chomsky normal form is how we modify the grammar to eliminate such situations.

It makes the parse tree a binary tree.
Each step will be productive, and we know it will not explode.
CNF form is not unique.

Example: Binary tree parse tree of CNF S \to AB | \epsilon \\ A \to a \\ B \to b \\

Example: CFG to CNF

\begin{aligned} S &\to ASA | aB \\ A &\to B|S \\ B &\to b|\epsilon \end{aligned}

Add new start variable (S_0)

\begin{aligned} \textcolor{green}{S_0} &\textcolor{green}{\to S} \\ S &\to ASA | aB \\ A &\to B|S \\ B &\to b|\epsilon \end{aligned}

Observations:
S \to ASA and S \to aB are not in CNF.
B \to b is in CNF.

Remove all epsilon transitions by a non-start variable.
- Add 1 rule for any occurrence going to epsilon.

Sub-Example: Removing an Epsilon Transitions

Suppose:

\begin{aligned} S \to BAB \\ B \to \epsilon \\ B \to b \\ A \to a \end{aligned}

We can move the epsilon into S, like so:

\begin{aligned} S \to B A B \\ S \to \epsilon A B \\ S \to B A \epsilon \\ S \to \epsilon A \epsilon \\ B \to b \\ A \to a \end{aligned}

As we can see, this generated four rules, as we had to account for every possibility of B in the right hand side going to epsilon, or not.

Let’s simplify by removing the useless epsilons.

\begin{aligned} S \to B A B \\ S \to A B \\ S \to B A \\ S \to A \\ B \to b \\ A \to a \end{aligned}

Or, as one line:

\begin{aligned} S \to B A B | A B | B A | A \\ B \to b \\ A \to a \end{aligned}

If you had something like S \to BABAB, the possibilities would be quite alot: S \to BABAB | ABAB | BAAB | BABA | AAB | BAA | ABA | AA

Removing B \to \epsilon

\begin{aligned} S_0 &\to S \\ S &\to ASA | aB | \textcolor{green}{a} \\ A &\to B|S|\textcolor{green}{\epsilon} \\ B &\to b \end{aligned}

Now, we have to remove A \to \epsilon

\begin{aligned} S_0 &\to S \\ S &\to ASA | aB | a | \textcolor{green}{ SA | AS | S } \\ A &\to B|S \\ B &\to b \end{aligned}

Remember: We can’t remove epsilon from start variable, as that’d change the language.

Remove unit rules

We can delete the useless S \to S.
anything to itself (e.g., A \to A) doesn’t change the language.

\begin{aligned} S_0 &\to S \\ S &\to ASA | aB | a | SA | AS \\ A &\to B|S \\ B &\to b \end{aligned}

Removing useless S_0 \to S

\begin{aligned} S_0 &\to \textcolor{green}{ASA | aB | a | SA | AS} \\ S &\to ASA | aB | a | SA | AS \\ A &\to B|S \\ B &\to b \end{aligned}

Remove A \to B

\begin{aligned} S_0 &\to ASA | aB | a | SA | AS \\ S &\to ASA | aB | a | SA | AS \\ A &\to S | \textcolor{green}{b} \\ B &\to b \end{aligned}

Remove A \to S

\begin{aligned} S_0 &\to ASA | aB | a | SA | AS \\ S &\to ASA | aB | a | SA | AS \\ A &\to b | \textcolor{green}{ASA | aB | a | SA | AS} \\ B &\to b \end{aligned}

Now, we just define new variables and rules to make the remaining rules follow CNF rules.

We’ll start by separating the terminals and variables by introducing T_a \to a

\begin{aligned} S_0 &\to ASA | \textcolor{green}{T_a B | T_a} | SA | AS \\ S &\to ASA | \textcolor{green}{T_a B | T_a} | SA | AS \\ A &\to b | ASA | \textcolor{green}{T_a B | T_a} | SA | AS \\ B &\to b \\ \textcolor{green}{T_a} &\textcolor{green}{\to a} \end{aligned}

Now, we’ll work on fixing the last non-CNF rule, ? \to ASA, by introducing a new variable (V_{SA} \to SA)

\begin{aligned} S_0 &\to \textcolor{green}{AV_{SA}} | T_a B | T_a | SA | AS \\ S &\to \textcolor{green}{AV_{SA}} | T_a B | T_a | SA | AS \\ A &\to b | \textcolor{green}{AV_{SA}} | T_a B | T_a | SA | AS \\ B &\to b \\ T_a &\to a \\ \textcolor{green}{$V_{SA}$} & \textcolor{green}{$\to SA$} \end{aligned}