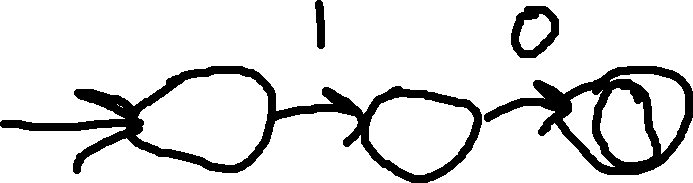NFA

NFA: Non-deterministic finite automata. A 5-tuple (Q, \Sigma, \delta, q_0, F), where

Q is a finite set of states
\Sigma is a finite alphabet
\delta: Q \times \Sigma_\epsilon \to P(Q) is the transition function
q_0 \in Q is the start state, and
F \subseteq Q is the set of accept states.

Example: DFA v.s. NFA

This is a DFA that recognizes 10 over \Sigma = \{ 0 , 1 \}

This is an NFA that does the same thing more succinctly.

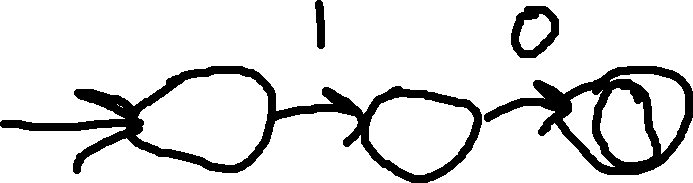
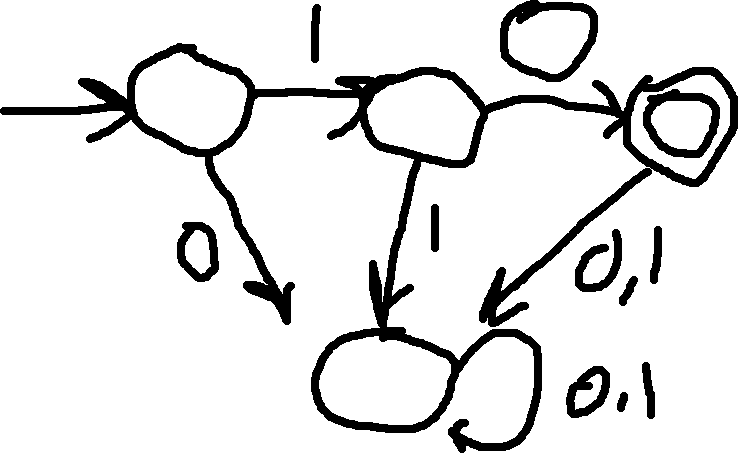
Suppose we want to recognize \{ 10, 00, 11 \}, the NFA is simply:

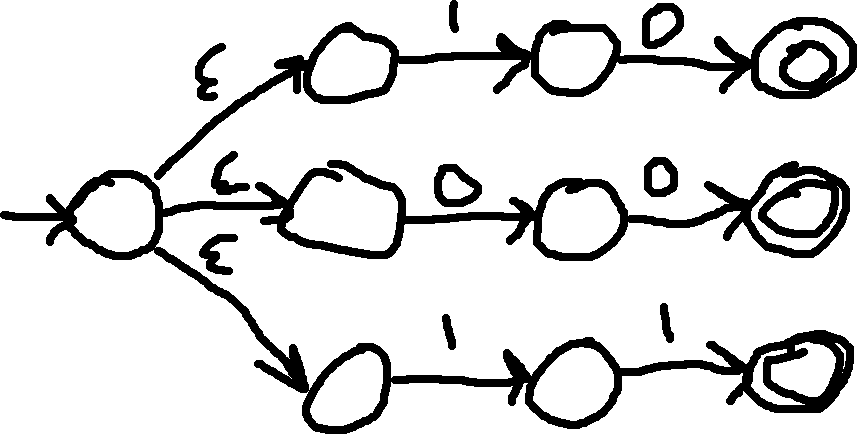
The union operation of three automata is way simpler in NFAs than DFAs, and NFAs are just simpler and less cluttered.

Designing NFAs

Find the essence of the problem
Write test strings
Design only the accepting path.
Test the NFA

Example: Write an NFA that accepts strings where the 3rd-to-last digit is 0. (Σ = {0, 1})

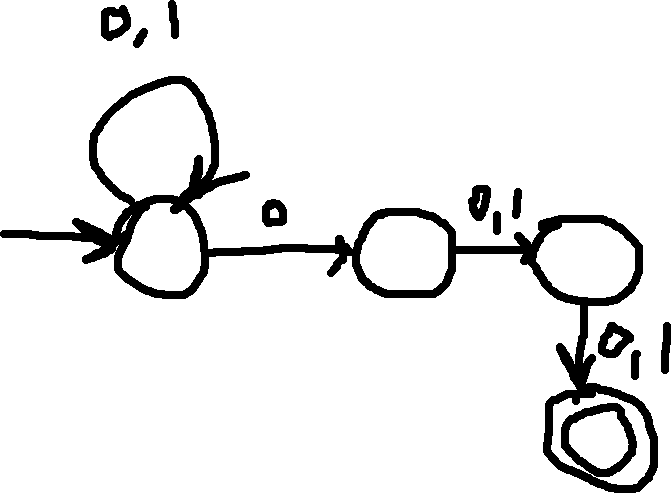
This NFA can be read as non-deterministically “guessing” to the accepting path.

Example: { w | w starts with 01, has even # of 1s, and ends with 0}

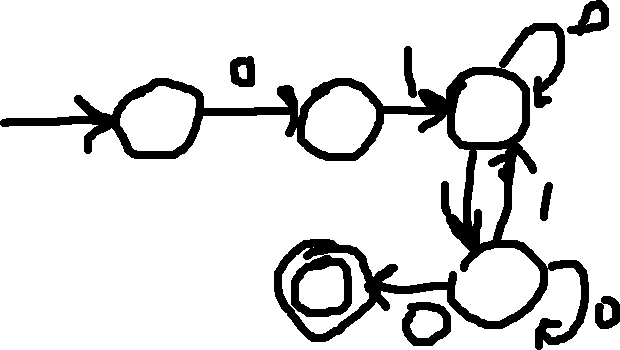
Notice how we do everything sequentially rather than branching with \epsilon.

Example: Complement of a Language

Example:
L = { w | w has a # of 1s divisible by 3}
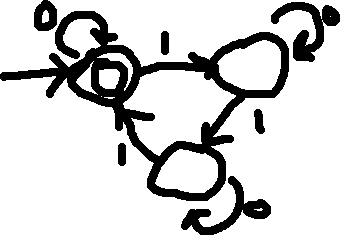
Q: How do we create a DFA to recognize the complement of L?
A: Simply flip the accepting states.
\bar{L} = U - L
U = \Sigma^*
Observations:
This only works for DFA, not NFA.

Strategies for Flipping an NFA:

You can flip the DFA, or
Write the NFA to find \bar{L} directly.

NFA \to DFA

We can turn any NFA into a DFA.

Steps:

Find the new start state (epsilon closure) E(S) = \text{ \{ q | q is reachable from $S$ via 0 or more $\epsilon$ transitions \} }
Find transitions (only consider reachable subsets from S’, \delta ' (R,a) = \cup_{r \in R} E ( \delta (r,a) ) \\ \small\textit{($\forall R \subseteq Q$)}
Mark accepting states F' = \text{ \{ R | q \in R, TODO \} }

Example

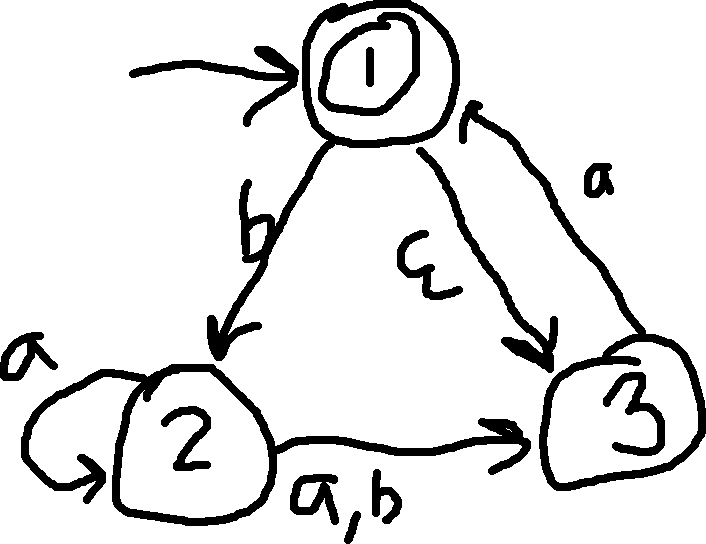
Q: Turn this NFA into a DFA.

Observations:

This NFA starts in either 1 or 3. (E(S) = { 1, 3 })
This is a transition table for the NFA that doesn’t have epsilon (because we’re trying to turn it into a DFA):

	a	b
1	\phi	{ 2 }
2	{ 2, 3 }	{ 3 }
3	{ 1, 3 }	\phi
{ 1, 3 }	\phi \cup { 1, 3 } = { 1, 3 }	\phi \cup { 2 } = { 2 }
{ 2 }	{ 2, 3 }	{ 3 }
{ 3 }	{ 1, 3 }	\phi
{ 2, 3 }	{ 1, 2, 3 }	{ 3 }
{ 1, 2, 3 }	{ 1, 2, 3 }	{ 2, 3 }

Q: Which ones are accepting?

A: All the ones with { 1 }

Q: How many states can the resulting DFA have?

A: |P(Q)|, or 2^{|Q|}

With the transition table, the DFA can now be constructed, starting at state { 1, 3 }.